
Mathematics in Class 11 becomes more advanced and detailed, and one of the most important chapters is Trigonometry Formulas for Class 11. These formulas not only help in solving complex problems in higher classes but also form the base for competitive exams like JEE, NEET, and other entrance tests.
In this blog article, we will cover all the essential Trigonometry Formulas for Class 11 in a simple and structured way so that students can easily revise and remember them during exams. also we provide Trigonometry Formulas for Class 11 and 12 pdf download free in our website ThinkSphereEdu.com
Table of Contents
Trigonometry Formulas For Class 11: Easy Tricks, Tables & Examples for Quick Learning
Trigonometry Ratios: (Trigonometry Formulas For Class 11)
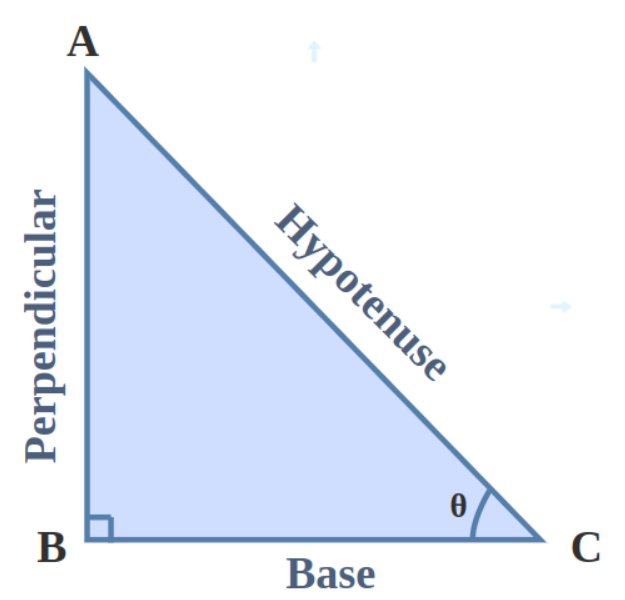
The word “trigonometry” is a 16th-century Latin derivative, and the concept was given by the Greek mathematician Hipparchus. Trigonometry is built on the relationship between the sides and angles of a right-angled triangle. The six (sine, cosine, tangent, cosecant, secant, and cotangent) basic trigonometric ratios are defined using the perpendicular (opposite side), base (adjacent side), and hypotenuse of the triangle.
Sine(sin θ): Perpendicular/Hypotenuse
Cosine(cos θ): Base/Hypotenuse
Tangent(Tan θ): Perpendicular/Base = Sin (θ)/cos (θ)
Cosecant(cosec θ): Perpendicular/Base = Sin (θ)/cos (θ)
Secant(sec θ): Hypotenuse/Base = 1/cos (θ)
Cotangent(cot θ): Base/Perpendicular =1/tan (θ)
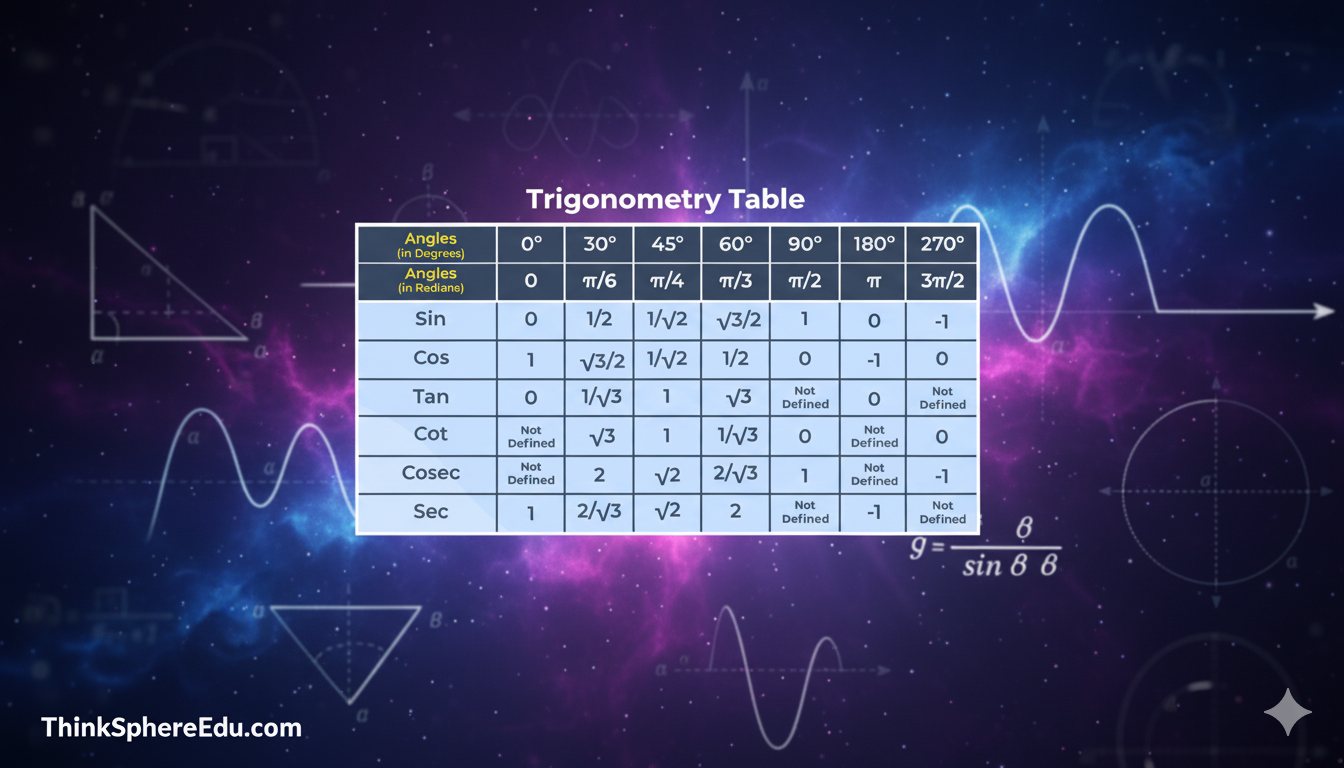
Trigonometry Table: (Trigonometry Formulas For Class 11)
These are the fixed values of trigonometric functions for common angles.
List of Trigonometry Formulas:
Here is the list of formulas for Class 11 students as per the NCERT curriculum. All the formulas of the trigonometry chapter are provided here for students to help them solve problems quickly.
Trigonometry Formulas:
| Trigonometry Formulas |
|---|
| sin(−θ) = −sin θ |
| cos(−θ) = cos θ |
| tan(−θ) = −tan θ |
| cosec(−θ) = −cosecθ |
| sec(−θ) = sec θ |
| cot(−θ) = −cot θ |
Product to Sum Formulas: (Trigonometry Formulas For Class 11)
A list of formulas for converting the product of two trigonometric functions into the sum or difference of two trigonometric functions is given as follows:
| Product to Sum Formulas |
|---|
| sin x sin y = 1/2 [cos(x–y) − cos(x+y)] |
| cos x cos y = 1/2[cos(x–y) + cos(x+y)] |
| sin x cos y = 1/2[sin(x+y) + sin(x−y)] |
| cos x sin y = 1/2[sin(x+y) – sin(x−y)] |
Sum to Product Formulas: (Trigonometry Formulas For Class 11)
| Sum to Product Formulas |
|---|
| sin x + sin y = 2 sin [(x+y)/2] cos [(x-y)/2] |
| sin x – sin y = 2 cos [(x+y)/2] sin [(x-y)/2] |
| cos x + cos y = 2 cos [(x+y)/2] cos [(x-y)/2] |
| cos x – cos y = -2 sin [(x+y)/2] sin [(x-y)/2] |
Angle Sum and Difference Formulas: (Trigonometry Formulas For Class 11)
Sum and Difference formulas are used to calculate the trigonometric function for those angles where a standard angle can’t be used. We have six main sum and difference formulas, which we mainly use in trigonometry.
These formulas allow you to break down or combine trigonometric functions of sums and differences of angles.
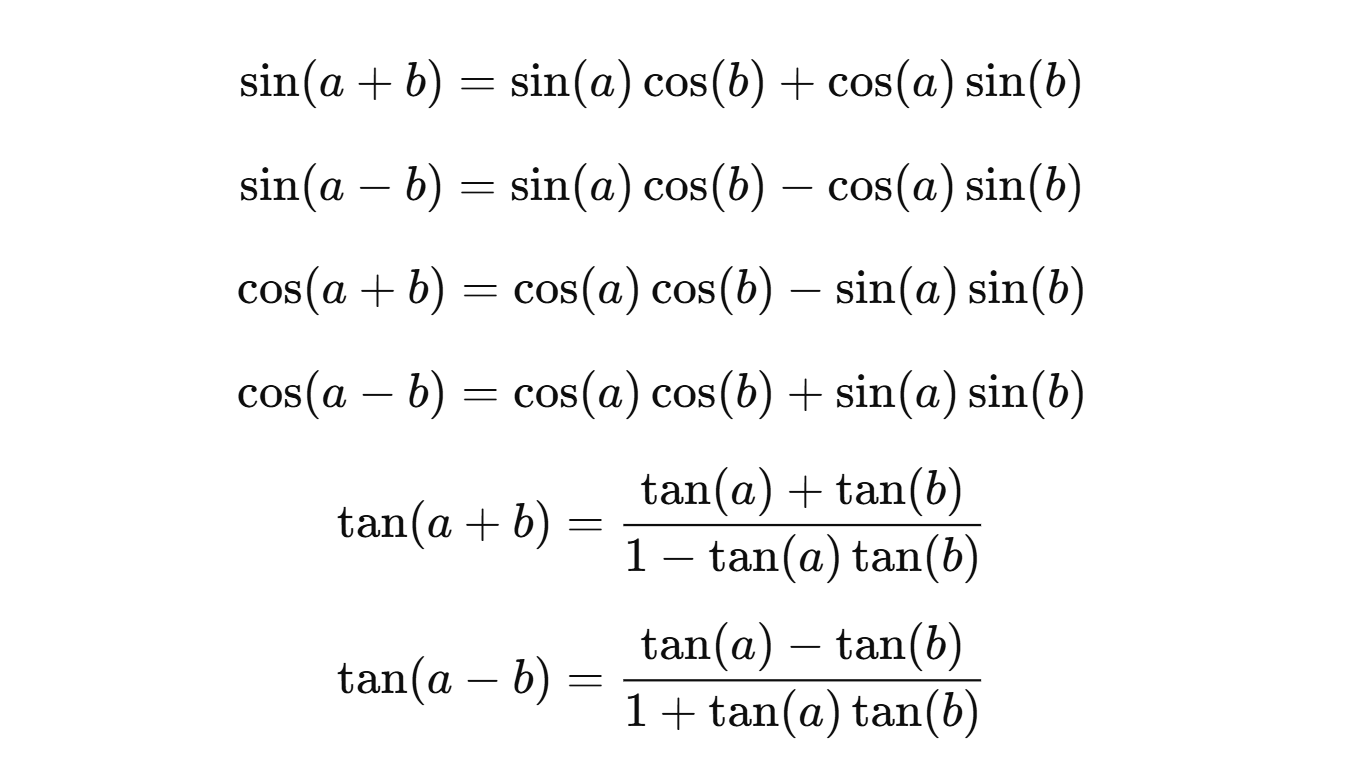
Double Angle Formulas: (Trigonometry Formulas For Class 11)
Double Angle Formulas are formulas in trigonometry to solve trigonometric functions where their angle is in the multiple of 2.
| Double Angle Formulas |
|---|
| sin (2θ) = 2sin(θ)cos(θ) = [2tan θ /(1+tan2θ)] |
| cos(2θ) = cos2(θ)−sin2(θ) = 1–2sin2θ = 2cos2θ–1 = [(1-tan2θ)/(1+tan2θ)] |
| tan(2θ) = 2tan(θ) / 1−tan2(θ) |
Half Angle Formulas: (Trigonometry Formulas For Class 11)
Half-angle formulas are used to find various values of trigonometric angles, such as for 15°, 75°, and others, they are also used to solve various trigonometric problems.
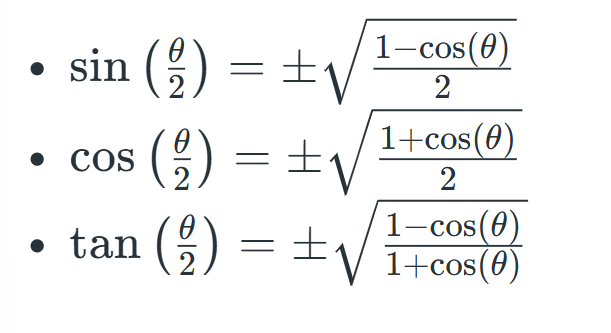
Triple Angle Formulas:
Trigonometric formulas containing three times the multiple of any angle θ are given as:

Identities:
| Identities |
|---|
| sin2 A + cos2 A = 1 |
| 1+tan2 A = sec2 A |
| 1+cot2 A = cosec2 A |
Sign of Trigonometric Functions in Different Quadrants:
| Quadrants | I | II | III | IV |
|---|---|---|---|---|
| Sin A | + | + | – | – |
| Cos A | + | – | – | + |
| Tan A | + | – | + | – |
| Cot A | + | – | + | – |
| Sec A | + | – | – | + |
| Cosec A | + | + | – | – |
Basic Trigonometric Formulas for Class 11:
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
sin (A+B) = sin A cos B + cos A sin B
sin (A -B) = sin A cos B – cos A sin B
Based on the above addition formulas for sin and cos, we get the following below formulas:
- sin(π/2-A) = cos A
- cos(π/2-A) = sin A
- sin(π-A) = sin A
- cos(π-A) = -cos A
- sin(π+A)=-sin A
- cos(π+A)=-cos A
- sin(2π-A) = -sin A
- cos(2π-A) = cos A
Solved Examples: (Trigonometry Formulas For Class 11)
Example – 1: If sin θ = 3/5, find cos θ.
Answer:
Use the identity sin²θ + cos²θ = 1
- sin²θ = (3/5)² = 9/25
- So, cos²θ = 1 − 9/25 = 16/25
- Therefore, cos θ = ±√(16/25) = ±4/5
- Final answer: cos θ = ±4/5 (depends on quadrant)
Example – 2: If sin θ = 3/5 and cos θ = 4/5, find tan θ.
Answer:
Use formula: tan θ = sin θ / cos θ
- tan θ = (3/5) / (4/5) = 3/4
Example – 3: Find sin(45° + 30°)
Answer:
Use formula: sin(A + B) = sin A cos B + cos A sin B
- sin 45° = √2/2, cos 30° = √3/2
- cos 45° = √2/2, sin 30° = 1/2
- sin(45° + 30°) = (√2/2)(√3/2) + (√2/2)(1/2)
- = √6/4 + √2/4 = (√6 + √2)/4
Example – 4: Find cos(2θ) if cos θ = 3/5
Answer:
Use formula: cos(2θ) = 2cos²θ − 1
- cos²θ = (3/5)² = 9/25
- cos(2θ) = 2(9/25) − 1 = 18/25 − 25/25 = −7/25
Example – 5: In a right triangle, opposite = 6, hypotenuse = 10. Find sin θ.
Answer:
sin θ = opposite / hypotenuse = 6/10 = 3/5
Example – 6: If tan θ = 2, find cot θ.
Answer:
cot θ = 1 / tan θ = 1/2
Example – 7: If cos θ = 0.8, find sin θ.
Answer:
Use formula: sin²θ + cos²θ = 1
- cos²θ = 0.64
- sin²θ = 1 − 0.64 = 0.36
- sin θ = √0.36 = 0.6
Example – 8: If sin 𝜃 = –4/5 and 𝜋 < 𝜃 < 3𝜋/2, find the value of all the other five trigonometric functions.
Answer:
Since, the value of theta ranges between 𝜋 < 𝜃 < 3𝜋/2, that means, 𝜃 lies in third quadrant.
Now, sin 𝜃 = –⅘ ⇒ cosec 𝜃 = 1/sin 𝜃 = – 5/4
∴ cot2 𝜃 = (cosec2 𝜃 – 1) = (25/16 – 1) = 9/16 ⇒ cot 𝜃 = ¾ (taking positive root as cot 𝜃 is positive in third quadrant)
tan 𝜃 = 1/cot 𝜃 = 4/3
Now, cos 𝜃 = cot 𝜃 sin 𝜃 = ¾ × (– ⅘ ) = – ⅗
∴ sec 𝜃 = 1/cos 𝜃 = – 5/3
Hence, all other trigonometric functions are cos 𝜃 = – ⅗, tan 𝜃 = 4/3, cot 𝜃 = ¾, sec 𝜃 = – 5/3 and cosec 𝜃 = – 5/4.
Example – 9: Find cos( – 870o)
Answer:
cos( – 870o) = cos(870o) [as cos ( –𝜃) = cos 𝜃 ]
= cos ( 2 × 360o + 150o)
= cos 150o [as cos (2n𝜋 + 𝜃) = cos 𝜃 ]
= cos ( 180o – 30o) = – cos 30o = – √3/2
Example – 10: Prove that sin x + sin 3x + sin 5x + sin 7x = 4sin 4x cox 2x cos x.
Answer:
Now, LHS = (sin 7x + sin x) + (sin 5x + sin 3x)
= 2 sin {(7x + x)/2} cos {(7x – x)/2} + 2 sin {(5x + 3x)/2} cos {(5x – 3x)/2}
= 2 sin 4x cos 3x + 2 sin 4x cos x
= 2 sin 4x (cos 3x + cos x)
= 2 sin 4x × 2 cos {(3x + x)/2} cos {(3x – x)/2}
= 2 sin 4x × 2 cos 2x cos x
= 4 sin 4x cos 2x cos x = RHS
